How do you find orthogonal trajectories of a family of curves?
Our method of finding the orthogonal trajectories of a given family of curves is therefore as follows: first, find the differential equation of the family; next, replace dy/dx by dx/dy to obtain the differential equation of the orthogonal trajectories; and finally, solve this new differential equation.
What is the orthogonal trajectory of the family of straight lines?
For example, the orthogonal trajectory of the family of straight lines defined by the equation y = kx, where k is a parameter (the slope of the straight line), is any circle having center at the origin (Figure 1): where is the radius of the circle. Figure 1.
What is an orthogonal trajectory to the family of circles?
A curve is said to be an orthogonal trajectory of a given family of curves if it is orthogonal to every curve in the family. For example, every line through the origin is an orthogonal trajectory of the family of circles centered at the origin.
What are orthogonal trajectories used for?
Orthogonal trajectories are used in mathematics, for example as curved coordinate systems (i.e. elliptic coordinates) and appear in physics as electric fields and their equipotential curves. If the trajectory intersects the given curves by an arbitrary (but fixed) angle, one gets an isogonal trajectory.
What is the trajectory of a family of curves?
The trajectory of a given family of curves is a curve that cuts every member of that family of curves according to a given law. Orthogonal Pathway. An orthogonal trajectory is one that cuts every member of a given family of curves at a right angle.
What is the formula of family of curves?
The differential equation of the family of curves v=Ar+B, where A and B are arbitrary constants is. d2vdr2+1rdvdr=0.
What is the equation for the orthogonal trajectories of the system?
The equation to the orthogonal trajectories of the system of parabolas y=ax2 is. x22+y2=c. x22−y2=c. x2+y22=c.
What is the equation for the trajectory of a straight line?
The straight-line equation can take many different forms. The straight line’s basic equation form seems to be y = mx + c; here, the m seems to be the straight line’s slope as well as c seems to be the point on the y – axis.
How do you know if lines are orthogonal?
Two lines are called orthogonal if they are perpendicular at the point of intersection.
What is meant by family trajectory?
Trajectories, however, are long-term patterns of stability and change and can include multiple transitions. Using longitudinal or retrospective data, family trajectories can be described by the complete sequence over time of union status, childbearing and eventually work status.
How do you find self orthogonal trajectories?
Replacing y/ by -1/y/, we get orthogonal trajectories as (x – y/y/)(-x/y/ – y) = -1/y/ which on simplification gives the same ODE. Hence self orthogonal. Geometrically: y2 = 4c(x + c): For c > 0 and c < 0 gives parabola in “opposite side” of the y-axis.
How do you find orthogonal circles?
If two circles intersect in two points, and the radii drawn to the points of intersection meet at right angles, then the circles are orthogonal, and the circles can be said to be perpendicular to each other. Thus they are also known as perpendicular circles.
How to find orthogonal trajectories of a family of curves?
To find the orthogonal trajectories to a family of curves, We find a differential equation satisfied by all of the curves solving for any constants in the description in terms of x and y.
What is the nature of orthogonal trajectory?
Orthogonal trajectory is a curve which intersects each and every member of a given family of curves at right angles. The given curve is a polynomial with constant, so it is quite easy for us to differentiate and integrate. We know that if we differentiate a constant it gives zero.
What is the benefit of orthogonality?
Orthogonality is a mathematical property that is beneficial for statistical models. It’s particularly helpful when performing factorial analysis of designed experiments. Orthogonality has various mathematic and geometric definitions.
Why is the trajectory a curved path?
Students have long been taught that all projectiles follow a curved path known as a parabola. The explanation is that as they fly, they cover distance both horizontally and vertically – but only the latter is affected by the force of gravity, which bends the path of the projectile into a parabola.
What is a curved trajectory called?
The path traced by a projectile that accelerates only in the vertical direction while moving at constant horizontal velocity is called a parabola. When air resistance can be neglected, the curved paths are parabolic and the paths are called trajectories.
What is a trajectory curve?
The trajectory is the curved path of the object in respect to its motion along with the gravity. Furthermore, we also refer to it as projectile motion. Besides, we are going to discuss trajectory, trajectory formula, its derivation, and solved examples.
What is family of curves functions?
In geometry, a family of curves is a set of curves, each of which is given by a function or parametrization in which one or more of the parameters is variable. In general, the parameter(s) influence the shape of the curve in a way that is more complicated than a simple linear transformation.
What is the envelope of a family of curves?
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope.
What is the differential equation of the family of plane curves?
The differential equation, which represents the family plane curves y = e^{cx}, is y’ = cyxy’- log y = 0x log y = yy’y log y = xy’
How do you derive orthogonal trajectories?
The orthogonal trajectories are curves along which heat will flow. Given the curves of heat flow y2−2xc=c2, we find the isotherms. 2yy′−2c=0⟹y′=c/y. We interpret Dt[x] to be 1, Dt[c] to be 0, and Dt[y] to represent the derivative.
What is the equation for orthogonal curves?
The orthogonal trajectories of the family of curves y=cxk are given by: x2+cy2= constant. x2+ky2= constant. x2−ky2= constant.
What is meant by family of curves?
A set of curves whose equations are of the same form but which have different values assigned to one or more parameters in the equations.
What is the basic formula for trajectory?
One common trajectory formula is the parametric equation: (x(t)=v₀cos(θ)t, y(t)=v₀sin(θ)t−(1/2)gt²), where v₀ is the initial velocity, θ is the launch angle, t is time, g is acceleration due to gravity, and x(t) and y(t) represent horizontal and vertical positions, respectively.
How to find the equation of trajectory?
Y=xtanθ−g×x22u2cos2θ is called equation of trajectory.
What is the equation for horizontal trajectory?
(b) The equation that describes the horizontal motion is x=x0+vxt.
What is the formula for orthogonal curves?
table of common derivative rules from analysis), and, because k = y/x2, a substitution of the latter in the former yields y′ = 2y/x. Solving this for the orthogonal curve gives the solution y2 + (x2/2) = k, which represents a family of ellipses (shown in red in the figure) orthogonal to the family of parabolas.
How do you find the envelope of a family of curves?
The envelope of a family of curves is a curve f(x,y,c)=0 whose equation is obtained by eliminating the parameter c from f(x,y,c)=0 and ∂f∂c=0, where ∂f∂c is the differential coefficient of f with respect to c, treating x and y as constants.
How do you find self orthogonal trajectories?
Replacing y/ by -1/y/, we get orthogonal trajectories as (x – y/y/)(-x/y/ – y) = -1/y/ which on simplification gives the same ODE. Hence self orthogonal. Geometrically: y2 = 4c(x + c): For c > 0 and c < 0 gives parabola in “opposite side” of the y-axis.
What is the formula for orthogonal projection?
We call ˆy the orthogonal projection of y onto W. Given an orthogonal basis {u1,…, up} for W, we have a formula to compute ˆy: ˆy = y·u1 u1·u1 u1 + ··· + y·up up·up up.
What is a family of orthogonal trajectories?
What is an orthogonal trajectory?
How to draw orthogonal trajectories for a family of curves?
How do you find orthogonal trajectories?
Have you ever wondered about the paths that intersect a family of curves at right angles? That’s precisely what orthogonal trajectories are all about. Imagine a bunch of curves, like a family portrait, and you’re tasked with finding the paths that cut through each member of this family at a perfect 90-degree angle. These intersecting paths, the orthogonal trajectories, reveal a hidden geometric relationship between the original curves.
Let’s break down this intriguing concept. A family of curves is a collection of curves that share a common property, defined by an equation. For example, a family of circles centered at the origin can be described by the equation *x² + y² = r²*, where *r* is the radius, which varies for each circle in the family.
Now, picture the orthogonal trajectories of this family of circles. These would be straight lines passing through the origin. Why? Because a line passing through the origin intersects any circle centered at the origin at a right angle. This is a simple yet illustrative example of how orthogonal trajectories can reveal interesting patterns within a family of curves.
Finding Orthogonal Trajectories: A Step-by-Step Guide
The process of finding orthogonal trajectories typically involves a couple of key steps:
1. Differential Equation: We begin by identifying the differential equation that represents the given family of curves. This equation captures the relationship between the slope of the tangent line at any point on a curve and the coordinates of that point. For instance, the differential equation for the family of circles mentioned earlier is *y’ = -x/y*.
2. Orthogonality Condition: The fundamental principle behind orthogonal trajectories is that the slopes of the original curve and its orthogonal trajectory are negative reciprocals of each other at their point of intersection. In mathematical terms, if *y’1* is the slope of the original curve and *y’2* is the slope of its orthogonal trajectory, then:
*y’1 * y’2 = -1*
3. Solving the Differential Equation: We substitute *y’1* with the expression obtained from the differential equation of the original curve and solve the resulting differential equation. This gives us the differential equation representing the family of orthogonal trajectories.
4. Integration and General Solution: Finally, we integrate the differential equation obtained in the previous step to find the general solution. This general solution, expressed in terms of *x* and *y*, represents the family of orthogonal trajectories.
Example: Finding the Orthogonal Trajectories of Parabolas
Let’s dive into a concrete example to solidify our understanding. Consider the family of parabolas given by the equation *y² = 4ax*. To find their orthogonal trajectories, we follow the steps outlined above.
1. Differential Equation: Differentiating both sides of the equation with respect to *x*, we get *2yy’ = 4a*. Solving for *y’*, we obtain the differential equation for the family of parabolas: *y’ = 2a/y*.
2. Orthogonality Condition: The slope of the orthogonal trajectories is the negative reciprocal of *y’*, which is *y’2 = -y/(2a)*.
3. Solving the Differential Equation: Replacing *y’1* with *2a/y* and *y’2* with *-y/(2a)* in the orthogonality condition *y’1 * y’2 = -1*, we get:
*(2a/y)* *(-y/(2a))* = -1*
Simplifying, we obtain the differential equation for the family of orthogonal trajectories: *y’ = -y/(2a)*.
4. Integration and General Solution: Integrating the differential equation, we get:
*∫ dy/y = -∫ dx/(2a)*
*ln|y| = -x/(2a) + C*
*y = Ce-x/(2a)*
This equation represents the family of orthogonal trajectories of the parabolas *y² = 4ax*, where *C* is an arbitrary constant. The orthogonal trajectories are exponential curves, reflecting the contrasting nature of parabolas and exponential functions.
Applications of Orthogonal Trajectories
Orthogonal trajectories find applications in various scientific and engineering fields:
Fluid Dynamics: Understanding the flow of fluids, particularly in the analysis of streamlines and equipotential lines.
Electromagnetism: Analyzing the relationship between electric and magnetic fields.
Heat Transfer: Investigating heat flow patterns.
Optics: Studying light propagation and the formation of images.
Mechanical Engineering: Designing and analyzing mechanical systems.
FAQs
Q: What are some other examples of orthogonal trajectories besides circles and parabolas?
A: Numerous families of curves have interesting orthogonal trajectories. For instance, the orthogonal trajectories of hyperbolas are ellipses, while the orthogonal trajectories of logarithmic spirals are also logarithmic spirals. The specific forms of the trajectories depend on the original family of curves.
Q: How are orthogonal trajectories used in real-world applications?
A: Orthogonal trajectories play a crucial role in understanding and modeling various physical phenomena. In fluid dynamics, they help visualize the paths of fluid particles, while in electromagnetism, they provide insights into the interplay between electric and magnetic fields. They also find applications in heat transfer, optics, and mechanical engineering, where they help analyze and optimize system performance.
Q: Is it always possible to find orthogonal trajectories for a given family of curves?
A: While orthogonal trajectories exist for many families of curves, it’s not guaranteed that they can be found for every family. Some families of curves may not have a well-defined differential equation, making it impossible to derive their orthogonal trajectories. Additionally, some families may have orthogonal trajectories that are too complex to find analytically.
Q: Can orthogonal trajectories be visualized using computer software?
A: Absolutely! Software like Mathematica, Maple, and MATLAB allow for the visualization and analysis of orthogonal trajectories. By inputting the differential equations of the original family of curves, these programs can generate plots of both the original curves and their orthogonal trajectories, providing a visual understanding of their relationship.
Orthogonal trajectories offer a fascinating window into the hidden geometric connections between different families of curves. Their applications across various scientific and engineering domains highlight their significance in understanding and modeling real-world phenomena. As we delve deeper into their intricacies, we uncover a deeper appreciation for the elegance and power of mathematical relationships in our world.
See more here: What Is The Orthogonal Trajectory Of The Family Of Straight Lines? | Orthogonal Trajectories Of Family Of Curves
How to find the orthogonal trajectories – Krista King Math
The orthogonal trajectories to a family of curves are the curves that intersect each member of the family at a perfectly perpendicular angle. So given a Krista King Math
Orthogonal Trajectory of $y^2 = kx^3$ – Mathematics
Find the orthogonal trajectories of the family of curves given by $x^2 + y^2 + 2Cy =1$. 2 Finding the equation of a line Mathematics Stack Exchange
Orthogonal Trajectories
Learn how to find orthogonal trajectories of a family of curves using partial differential equations or ordinary differential equations. See examples, definitions, and algorithms math24.net
2.4 Some Applications 1. Orthogonal Trajectories – University of
A curve that intersects each member of a given family of curves at right angles (orthog-onally) is called an orthogonal trajectory of the family. Each line in (c) is an orthogonal UH – Department of Mathematics
Orthogonal trajectories, MATH 3410 – Differential equations for …
Learn how to find orthogonal trajectories of a family of curves using differential equations. See examples of circles, parabolas and ellipses and their Department of Physics
4.5: Applications to Curves – Mathematics LibreTexts
A curve is said to be an orthogonal trajectory of a given family of curves if it is orthogonal to every curve in the family. For example, every line through the origin is an orthogonal trajectory of the family of circles Mathematics LibreTexts
Orthogonal trajectory | Linear Motion, Vector Calculus & Geometry
Learn about orthogonal trajectories, families of curves that intersect another family of curves at right angles. Find out how to derive the differential equation for the orthogonal Britannica
Orthogonal trajectories – MATHCURVE.COM
Two families of curves are said to be orthogonal when at every point common to a curve of each family, the tangents are orthogonal, and one of the families is said to be composed of the orthogonal trajectories of MATHCURVE.COM
Orthogonal trajectory – Wikipedia
In mathematics, an orthogonal trajectory is a curve which intersects any curve of a given pencil of (planar) curves orthogonally. For example, the orthogonal trajectories of a Wikipedia
See more new information: pilgrimjournalist.com
Orthogonal Trajectories – Differential Equations
Orthogonal Trajectories And Differential Equations – Calculus 2
Problem On Orthogonal Trajectory Of Family Of Curves / Problem-4
Finding Orthogonal Trajectories
Orthogonal Trajectories, Application Of First Order Differential Equations
Link to this article: orthogonal trajectories of family of curves.
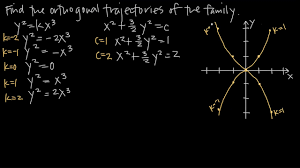
See more articles in the same category here: https://pilgrimjournalist.com/wiki/